下载:
-
静脉用药调配中心（pharmacy intravenous ad-mixture services, PIVAS）是专为临床提供静脉用药调配服务的药品调剂部门。随着PIVAS业务的发展，人员配置、时间分配等诸多管理话题备受关注[1-4]。通常资源配置、时间管理及工作方式等管理决策的落地均需结合工作量情况，这是因为工作量不仅可用于绩效考核，也可用于衡量需求与供给是否匹配，是调整工作强度和实现最佳调配实践过程的关键组成部分，并且对静脉药物调配服务的提供有着深远的影响（诸如人员倦怠、供应短缺导致治疗延误、调配差错等不期望的结局）[5]。因而，客观选择能够代表工作量的关键指标进行准确量化及特征分析，对PIVAS工作模式的制定和优化具有重要意义。
据上海市药学会医院药学专委会PIVAS学组2022年统计数据显示，以长期医嘱（执行两次以上的定期医嘱）为调配工作类型的上海医疗机构高达97.4%，其中31.6%的机构仅接收执行此项工作[6]。因此，客观上存在管理决策匹配至长期医嘱工作的需求，以达到解决临床用药需求、保证准点交付及提高服务质量的目的。然而，现阶段PIVAS管理决策的匹配多依赖于实操经验，缺乏可靠的理论依据，主要原因是长期医嘱工作量特征没有得到细致量化的分析并在文献中进行报道。
按日期汇总的PIVAS长期医嘱工作量是典型的时间序列，而时间序列分析法目前较为成熟，已在金融、气象、医学等领域得到广泛应用[7]。该技术不仅可通过分解法识别变量存在的周期性、循环性、趋势性等变化特征，还可根据历史数据特征进行回归分析或机器学习等模型的构建及预测[8]。因此，本研究借助时间序列分析法对PIVAS长期医嘱工作量数据进行特征分析及预测，以期为PIVAS工作模式的制定提供参考。
-
数据来自复旦大学附属中山医院东院区PIVAS，选取2020年7月至2021年6月的长期医嘱日工作量整年周期数据，进行时间序列分析及预测模型构建，选取2021年7月的数据用于模型预测准确度的验证。
-
利用SPSS 25.0软件对获得的工作量数据绘制时间序列图。通过局部加权回归拟合函数（loess function）对序列进行季节和趋势分解[9]，初步描述分析数据的长期趋势、季节波动、循环波动、不规则波动等重要特征。
-
基于数据的趋势性、季节性或平稳性假设，通过制定一个数学模型来捕捉现有的动态关系，理解数据生成过程，并可能在提出的假设限制内进行预测。传统的建模方法包括指数平滑、移动平均、多元线性回归和自回归综合移动平均等，可利用 SPSS 25.0软件直接进行统计分析以识别适合的建模方法。
-
预测模型的构建方法大多需要序列平稳假设的前提，即序列的均值和方差等基本统计量随时间保持不变。采用Eviews 11对时间序列数据进行单位根检验（ADF检验），以观察平稳性，若检验为非平稳序列则需进行差分运算，转化为平稳时间序列。
-
应用SPSS 25.0软件中的“时间序列建模器”进行建模。根据序列的波动特征、自相关系数（ACF）及偏自相关系数（PACF）识别模型，通过试误法进行模型参数估计。以Ljung-Box统计量检验残差是否符合常态分配的基本假设，P>0.05说明模型构建成功；当拟合度（平稳R2和R2）>0.05、残差的ACF和PACF图无规律及拟合值与实际值的平均绝对误差（MAPE）<10%时，说明模型拟合效果好。
-
利用所构建的时间序列模型进行样本外预测，并与实际值比较，通过相对误差百分比验证模型的预测能力。相对误差百分比(δ)= (预测值−实际值)/实际值×100％，δ<10%时说明模型预测有效。
-
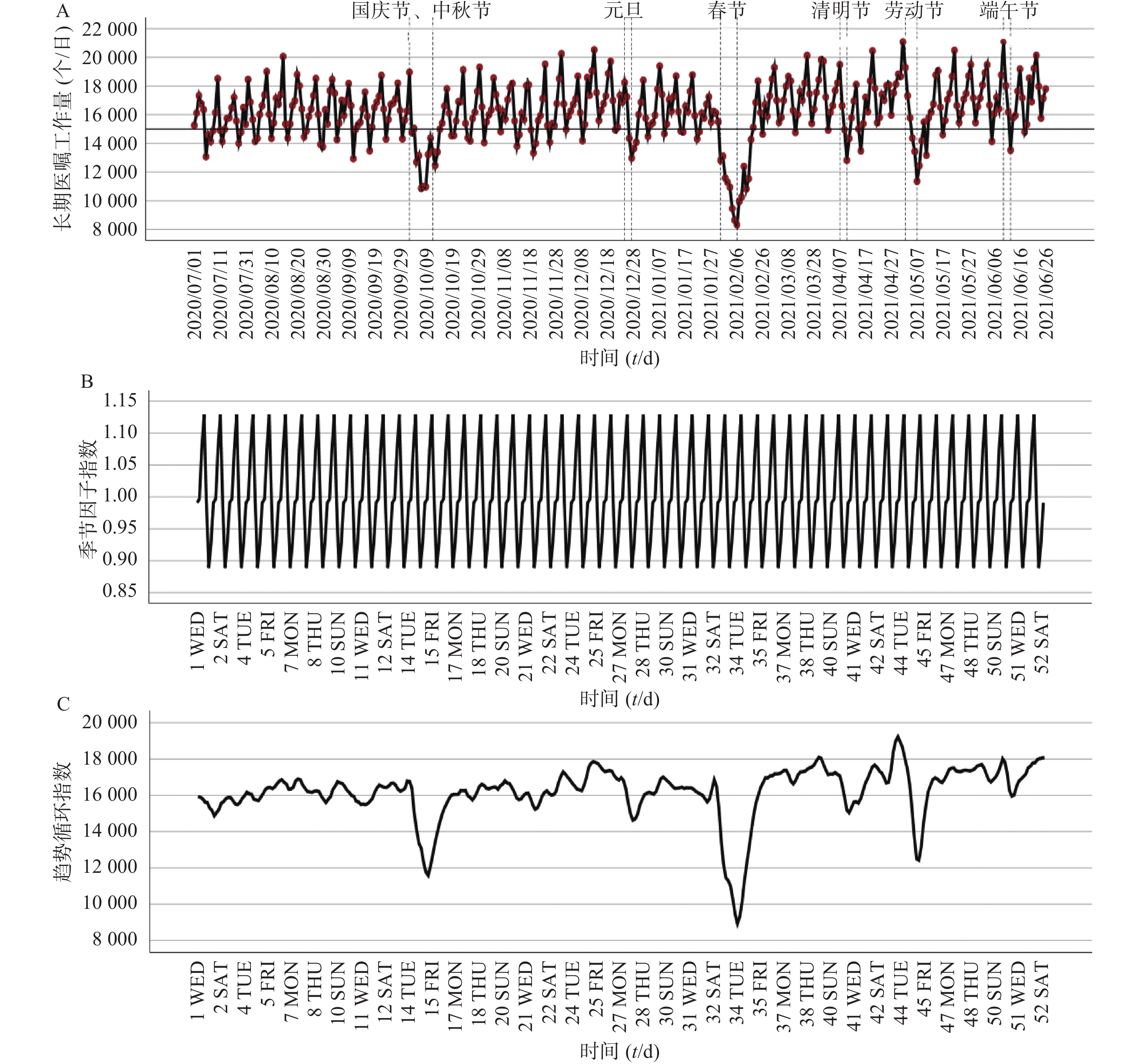
利用复旦大学附属中山医院东院区2020年7月至2021年6月PIVAS长期医嘱工作量数据，绘制原始序列图并进行时间序列分解。图1A为原始序列，由365个数据集成，工作量日均值为16188.55个，且整年数据基本维持在16000振幅波动，但极值（8326~21302）间相差约为2.5倍，说明PIVAS长期医嘱工作量的波动存在规律性及异常性等特征。时间序列分解结果表明：序列具有周期性、缓慢上升趋势及不规则变动等特征。图1B为季节因子序列，说明长期医嘱工作量数据遵循以7 d为周期的变动规律，单周期波动总体存在周一（谷值）至周六（峰值），先上升而后下降的模式；图1C为循环趋势序列，提示不规则变动均发生在国家法定节假日期间，且假期越长序列的不规则性越明显；工作量总体呈现缓慢上升趋势且在节假日前迎来高峰。
图 1 PIVAS长期医嘱工作量波动序列
-
对PIVAS长期医嘱日工作量时间序列进行单位根ADF检验，检验结果表明：ADF统计值为−5.922 144，小于1%（−3.448 518）、5%（−2.869 442）、10%（−2.571 047）显著性水平的临界值（P<0.000 01），说明工作量时间序列不存在单位根，为平稳序列，符合时间序列模型构建要求。
-
根据原始序列图的波动特征，将趋势及季节因素均纳入考虑的简单季节性模型、温特斯加法模型或温特斯乘法模型建模，最终选取温特斯乘法模型。该模型Ljung-Box统计量的显著性值大于0.05（P=0.060），表明模型正确，说明所观测的序列中不存在模型无法解释的结构（图2）。拟合参数平稳R2=0.549、R2=0.777、残差的ACF和PACF图无规律性（图2A）；工作量拟合图拟合值波动趋势与实际值基本吻合（图2B），且 MAPE=4.45%（<10%），说明模型拟合效果好。
图 2 基于温特斯乘法模型残差的ACF、PACF（A）及工作量预测值与实际值拟合图（B）
-
工作量预测结果的波动特征呈现明显的周期性特征（图2B）。表1显示，2021年7月长期医嘱工作量的短期预测误差处于10%之内，且平均相对偏差为3.81%，说明模型有效。
表 1 2021年7月静脉用药调配中心实际工作量与预测工作量的比较
日期 实际工作量(袋) 预测工作量(袋) 相对误差(%) 2021-07-01 17467 18161 3.97 2021-07-02 19722 19495 −1.15 2021-07-03 18732 20386 8.83 2021-07-04 17317 17890 3.31 2021-07-05 15412 15962 3.57 2021-07-06 16238 16726 3.01 2021-07-07 18796 17942 −4.54 2021-07-08 16766 18197 8.54 2021-07-09 20154 19534 −3.08 2021-07-10 18697 20427 9.25 2021-07-11 17521 17926 2.31 2021-07-12 15295 15994 4.57 2021-07-13 16088 16759 4.17 2021-07-14 17495 17978 2.76 2021-07-15 17968 18233 1.47 2021-07-16 20266 19573 −3.42 2021-07-17 19986 20468 2.41 2021-07-18 17335 17962 3.62 2021-07-19 14618 16026 9.63 2021-07-20 16982 16793 −1.11 2021-07-21 16879 18014 6.72 2021-07-22 18567 18270 −1.60 2021-07-23 20632 19612 −4.94 2021-07-24 20689 20508 −0.87 2021-07-25 16998 17997 5.88 2021-07-26 16086 16058 −0.17 2021-07-27 16675 16826 0.91 2021-07-28 17929 18049 0.67 2021-07-29 17634 18306 3.81 2021-07-30 20090 19651 −2.19 2021-07-31 21755 20549 −5.54 -
前期通过文献查阅梳理出可以代表工作量的常见指标[10-12]，主要包括“日调配时间”、“日输液袋量”、“日用药支数”及“日注射剂总量”。通过相关性分析（表2）发现，指标间均存在显著正相关，说明指标间可能存在某种联系，一定程度均可以代表工作量。尽管按输液量（袋数）计算的日调配量是现今PIVAS工作量评价共识[12]，但该指标更适用于周转过程的统计，并不能较好体现输液制备过程的工作难易程度。此外，“日调配时间”指标统计过程的规范化程度，以及“日用药支数”指标忽略大容量注射剂（输液）统计导致的大容量注射剂工作量缺失，均可能引发工作量特征量化的准确性争议。因此，基于指标参数获取的准确性、PIVAS长期医嘱工作结构、过程及结果的综合考虑，本研究最终选择“日注射剂总量”（即每日注射剂总量，包含大容量注射剂）作为长期医嘱工作量指标。该指标参数不仅可直接从医院信息系统（HIS系统）获得，而且一定程度体现了工作强度及药品使用情况，有助于建立管理和PIVAS医嘱工作量之间的统计关联。
表 2 主要指标的相关系数矩阵（n=365）
变量 均值 标准差 日调配
时间
（min）日输液量
（袋）日用药量
（支）日调配时间
(min)3045.96 399.749 日输液量
(袋)3087.49 312.444 0.908** 日用药量
(支)13101.06 1775.484 0.839** 0.879** 日注射剂
总量(个)16188.55 2055.580 0.863** 0.911** 0.997** 注：**P<0.01。 研究发现长期医嘱工作量波动具有明显的周期性、受节假日因素影响的不规则变动以及不明显的缓慢增长趋势等特征。有意思的是，多项研究证实门急诊日诊量波动具有同样的波动特征[13-14]，说明医院工作模式可能是影响医疗机构内日工作量波动的关键因素。需要注意的是，PIVAS药学服务在医疗机构中属于下游服务节点，存在滞后性，从而导致工作量波动特征存在周一谷值和周六峰值等现象。此外，波动性还可能受临床患者住院时间的主观因素影响，包括入院期、出院期、床位周转率、化疗周期以及患者手术择期选择等因素[15]。后续有必要采用相关性分析等手段进一步验证假设，从而建立与临床数据间的联系，以便更好地为临床服务。随后课题组将波动特征规律运用到PIVAS运营管理中，制订了一些措施，取得较好成效。如：（1）周六及节假日初期充足准备，中后期直至工作日来临适当减少，一旦进入工作日周期又逐步增加的资源配备；（2）通过周排班模式合理搭配、均衡人力配置原则来统筹协调人力资源；（3）每周周一盘点，周二物资采购，周五补充，来保障物资供应以应对周内工作量攀升压力。
简单季节模型、温特斯乘法模型均能提供准确预测，基于贝叶斯信息准则最小原则选择温特斯乘法模型。温斯特乘法模型具有实践轻松简单、高预测精度的优点，然而仍存在一定的局限性，体现在其主要通过提取时间序列中季节变动及长期趋势因素建模，对于元旦、春节等节假日信息提取不足，从而可能降低预测值的精确度。导致这一结果的根本原因是节假日的时间跨度不明确，后期将收集更多长期医嘱工作量数据以便丰富数据，考虑构建长期记忆模型以便将元旦等节假日因素纳入模型中，从而使预测更精准。
综上所述，本研究所采用的时间序列分析法为科学分析与预测PIVAS长期医嘱工作量变化提供了思路，该方法实现简单，可行性强，准确度高，对药房管理有一定指导和实践意义。然而，真实世界中的数据存在固有的复杂性，不存在适用于任何环境的通用模型，如受天气或流感爆发等因素影响时，可进行及时的短期分析以实现更精确的近期预测。
Fluctuation analysis and prediction of intravenous medication dispensing workload based on time series analysis method
-
摘要:
目的 探讨静脉用药调配中心（pharmacy intravenous admixture services，PIVAS）长期医嘱工作量的波动特征，构建以日为单位频次的工作量波动预测模型，为PIVAS工作模式的调整提供参考。 方法 选取复旦大学附属中山医院东院区PIVAS2020年7月至2021年6月长期医嘱日工作量数据，采用时间序列分析法分析工作量波动特征并构建预测模型，通过拟合参数及预测结果验证模型精度。 结果 PIVAS长期医嘱日工作量数据波动具有周期性、短期缓慢上升和不规则变动等特征；采用温特斯乘法模型拟合序列，Ljung-Box统计量的显著性值（P值）为 0.060（P > 0.05），R2 = 0.777，拟合值与实际值的平均绝对误差为4.45%，表明模型拟合精度高；预测结果与实测结果平均相对偏差为3.81%，说明模型预测有效。 结论 时间序列分析法可用于PIVAS长期医嘱工作量的分析预测，但因医嘱工作量存在周期性、不规则变动等波动规律，故需根据工作量波动特征及预测结果调整工作模式，以保障PIVAS高效运营。 Abstract:Objective To explore the fluctuation characteristics of long-term doctor's order workload in pharmacy intravenous admixture services (PIVAS) and build a daily workload fluctuation prediction model and provide reference for the adjustment of PIVAS work mode. Methods Daily workload data of long-term doctor’s orders from PIVAS in the East Campus of Zhongshan Hospital affiliated to Fudan University from July 2020 to June 2021 were selected , and the time series analysis method was used to analyze the workload fluctuation characteristics and a prediction model was established. The accuracy of the model was verified by fitting parameters and prediction results. Results The fluctuation of PIVAS long-term doctor's daily workload data had the characteristics of periodicity, short-term slow rise and irregular variation. The Winters multiplier model was used to fit the series with R2 = 0.777, the significance value of Ljung-Box statistic value (P value) was 0.060, and the mean absolute error percentage between the fitted and actual values was 4.45%, indicating that the model fitting accuracy was high. The average relative deviation between the predicted and actual results was 3.81%, indicating that the model prediction was effective. Conclusion The model constructed in this study could be used for the analysis and prediction of long-term doctor's orders workload of PIVAS. However, because the workload of doctor's orders has fluctuations such as periodicity and irregular changes, it is necessary to adjust the working model according to the fluctuation characteristics of the workload and the prediction results to ensure the efficient operation of PIVAS. -
表 1 2021年7月静脉用药调配中心实际工作量与预测工作量的比较
日期 实际工作量(袋) 预测工作量(袋) 相对误差(%) 2021-07-01 17467 18161 3.97 2021-07-02 19722 19495 −1.15 2021-07-03 18732 20386 8.83 2021-07-04 17317 17890 3.31 2021-07-05 15412 15962 3.57 2021-07-06 16238 16726 3.01 2021-07-07 18796 17942 −4.54 2021-07-08 16766 18197 8.54 2021-07-09 20154 19534 −3.08 2021-07-10 18697 20427 9.25 2021-07-11 17521 17926 2.31 2021-07-12 15295 15994 4.57 2021-07-13 16088 16759 4.17 2021-07-14 17495 17978 2.76 2021-07-15 17968 18233 1.47 2021-07-16 20266 19573 −3.42 2021-07-17 19986 20468 2.41 2021-07-18 17335 17962 3.62 2021-07-19 14618 16026 9.63 2021-07-20 16982 16793 −1.11 2021-07-21 16879 18014 6.72 2021-07-22 18567 18270 −1.60 2021-07-23 20632 19612 −4.94 2021-07-24 20689 20508 −0.87 2021-07-25 16998 17997 5.88 2021-07-26 16086 16058 −0.17 2021-07-27 16675 16826 0.91 2021-07-28 17929 18049 0.67 2021-07-29 17634 18306 3.81 2021-07-30 20090 19651 −2.19 2021-07-31 21755 20549 −5.54 
下载: 导出CSV
表 2 主要指标的相关系数矩阵（n=365）
变量 均值 标准差 日调配
时间
（min）日输液量
（袋）日用药量
（支）日调配时间
(min)3045.96 399.749 日输液量
(袋)3087.49 312.444 0.908** 日用药量
(支)13101.06 1775.484 0.839** 0.879** 日注射剂
总量(个)16188.55 2055.580 0.863** 0.911** 0.997** 注：**P<0.01。
下载: 导出CSV
-
[1] 耿魁魁, 徐文, 魏泽元, 等. 医疗机构静脉用药调配中心智能化发展现状与展望[J]. 中国医院用药评价与分析, 2020, 20(6):756-759. doi: 10.14009/j.issn.1672-2124.2020.06.031 [2] MI W J, LI L, ZHANG Y, et al. Chinese centralised intravenous admixture service (CIVAS), an emerging pharmaceutical industry: survey of the recent advances of CIVAS in China[J]. Eur J Hosp Pharm,2018,25(3):165-168. doi: 10.1136/ejhpharm-2016-001154 [3] GAO T, ZHANG X Z, GURD B, et al. From self-management to a systemized process: the implementation of lean management in a Chinese hospital’s pharmacy intravenous admixture services center[J]. Leadersh Health Serv (Bradf Engl),2020,33(4):325-337. doi: 10.1108/LHS-12-2019-0085 [4] FARLEY M T, SEGAL R. Implementation and evaluation of a flexitime program involving pharmacy i. v. admixture technicians[J]. Hosp Pharm,1987,22(3):261-264. [5] FISHBEIN D, NAMBIAR S, MCKENZIE K, et al. Objective measures of workload in healthcare: a narrative review[J]. Int J Health Care Qual Assur,2019,33(1):1-17. doi: 10.1108/IJHCQA-12-2018-0288 [6] 鲁国璋, 张建中. 上海市39家医疗静脉用药调配中心建设与运行情况调研[J]. 上海医药, 2023, 44(15):50-55. doi: 10.3969/j.issn.1006-1533.2023.15.013 [7] ORT J, HAKVOORT K, NEULOH G, et al. Foundations of time series analysis[J]. Acta Neurochir Suppl,2022,134:215-220. [8] WEISS T W, ASHTON C M, WRAY N P. Forecasting areawide hospital utilization: a comparison of five univariate time series techniques[J]. Health Serv Manage Res,1993,6(3):178-190. doi: 10.1177/095148489300600304 [9] ORDU M, DEMIR E, TOFALLIS C. A comprehensive modelling framework to forecast the demand for all hospital services[J]. Int J Health Plann Manage,2019,34(2):e1257-e1271. [10] 刘文巧, 黄燕, 李开应. 应用六西格玛方法缩短静脉用药调配中心长期医嘱调配时间[J]. 中国农村卫生, 2021, 13(8):51-52. doi: 10.3969/j.issn.1674-361X.2021.08.032 [11] 陈红英, 陶娌娜, 张杰, 等. 合理使用注射剂规格与药物经济性和安全性探讨分析[J]. 实用药物与临床, 2019, 22(2):220-224. doi: 10.14053/j.cnki.ppcr.201902027 [12] 国家卫生健康委. 静脉用药调配中心建设与管理指南(试行)[S/OL]. (2021-12-10)[2022-01-20]. http://www.gov.cn/zhengce/zhengceku/202112/21/Content_5663666.htm. [13] JONES S S, THOMAS A, EVANS R S, et al. Forecasting daily patient volumes in the emergency department[J]. Acad Emerg Med,2008,15(2):159-170. doi: 10.1111/j.1553-2712.2007.00032.x [14] LUO L, LUO L, ZHANG X L, et al. Hospital daily outpatient visits forecasting using a combinatorial model based on ARIMA and SES models[J]. BMC Health Serv Res,2017,17(1):469. doi: 10.1186/s12913-017-2407-9 [15] MCCOY T H Jr, PELLEGRINI A M, PERLIS R H. Assessment of time-series machine learning methods for forecasting hospital discharge volume[J]. JAMA Netw Open,2018,1(7):e184087. doi: 10.1001/jamanetworkopen.2018.4087 -
点击查看大图
图(2) / 表(2)
计量
- 文章访问数: 1767
- HTML全文浏览量: 995
- PDF下载量: 15
- 被引次数: 0
